6033. Kastenlauf
Once every year, Jo
and his friends want to visit the local fair in Erlangen, called Bergkirchweih.
This year, they want to make a Kastenlauf (box run). They start at Jo’s home
and have one box (Kasten) of beer (with twenty bottles). As they are
very thirsty, they drink one bottle of beer every 50 meters.
As the way from
Jo's home to the Bergkirchweih is pretty long, they
need more beer than they have initially. Fortunately, there are stores selling
beer on the way. When they visit a store, they can drop their empty bottles and
buy new bottles, but their total number of full bottles will not be more than
twenty (because they are too lazy to carry more than one full box).
You are given the
coordinates of the stores, of Jo's home and of the location of the Bergkirchweih.
Write a program to determine whether Jo and his friends can happily reach the
Bergkirchweih, or whether they will run out of beer on the way.
Input. First line
contains the number of test cases t (t ≤ 50). Each
test case starts with one line, containing the number n (0 ≤ n
≤ 100) of stores selling beer. The next n + 2 lines contain
(in this order) the location of Jo’s home, of the stores, and of the
Bergkirchweih. The location is given with two integer coordinates x and y
(both in meters, -32768 ≤ x, y ≤ 32767). As
Erlangen is a rectangularly laid out city, the distance between two locations
is the difference of the first coordinate plus the difference of the second
coordinate (also called Manhattan-Metric).
Output. For each test case
print one line, containing either “happy” (if Jo and his friends can happily
reach the Bergkirchweih), or “sad” (if they will run out of beer on the way).
|
Sample input |
Sample output |
|
2 2 0 0 1000 0 1000 1000 2000 1000 2 0 0 1000 0 2000 1000 2000 2000 |
happy sad |
SOLUTION
graphs – depth first search
Algorithm analysis
Since the
number of bottles that guys can carry with them is 20, and every 50 meters one
should drink one
bottle, they can only move between stores, the distance between which is no
more than 20 * 50 = 1000 meters.
Let’s build a graph with Joe’s house, shops and Bergkirchweich as its vertices. An
edge between the vertices is
present if only the distance between them is not more than 1000 meters. That
is, the undirected edges indicate the possible paths of movement for Joe and
his friends.
Start the depth
first search from the Joe’s house. If it is possible to reach Bergkirchweich from it,
then friends will be happy, otherwise they will not.
Example
For the
first and the second
examples, the graph will look like this:
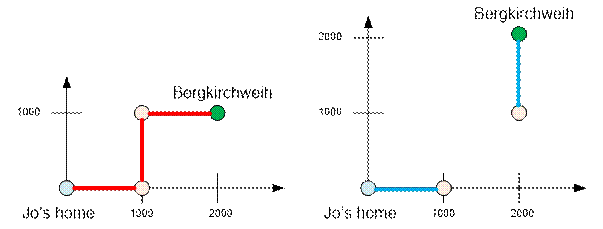
In the
first example, Joe and his friends can reach the Bergkirchweich fair. In the
second, no. You can only move between those vertices of the graph, the distance
between which is no more than 1000 meters.
Algorithm
realization
Store the coordinates in (x[i],
y[i]). Declare the movement graph g.
#define MAX 110
int x[MAX], y[MAX];
vector<vector<int>
> g;
vector<int> used;
Depth first search from the vertex v.
void dfs(int
v)
{
used[v] = 1;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i];
if (!used[to]) dfs(to);
}
}
The main part of the program. Read the input data.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
Since the input data contains several tests, clear the
arrays.
g.clear();
g.resize(n+2);
used.clear();
used.resize(n+2);
Read the coordinates of Jo’s
home (x[0], y[0]), shops and Bergkirchweih (x[n – 1], y[n – 1]).
for(i = 0; i < n + 2; i++)
scanf("%d %d",&x[i],&y[i]);
Build a
graph of possible movements. From the vertex
(x[i], y[i]) you can go to the vertex (x[j], y[j]) if only the distance between them is
no more than 1000 meters. The graph is undirected. The metric is Manhattan.
for(i = 0; i < n + 2; i++)
for(j = i + 1; j < n + 2; j++)
if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)
{
g[i].push_back(j);
g[j].push_back(i);
}
Start from
Joe’s house. Start the depth first search from the vertex 0.
dfs(0);
If Bergkirchweich is reachable, then output “happy”,
otherwise output “sad”.
if (used[n + 1]) puts("happy");
else puts("sad");
}
Algorithm
realization – adjacency matrix
#include <stdio.h>
#include <string.h>
#define MAX 110
int tests, n, i, j;
int x[MAX], y[MAX];
int g[MAX][MAX], used[MAX];
int abs(int
x)
{
return (x < 0) ? -x : x;
}
void dfs(int
v)
{
used[v] = 1;
for(int i = 0; i <
n + 2; i++)
if (g[v][i] && !used[i]) dfs(i);
}
int main(void)
{
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
memset(g,0,sizeof(g));
memset(used,0,sizeof(used));
// 0 = Jo's house, start
// 1 .. n - stores selling beer
// n+1 - Bergkirchweih, finish
for(i = 0; i < n + 2; i++)
scanf("%d %d",&x[i],&y[i]);
for(i = 0; i < n + 2; i++)
for(j = i + 1; j < n + 2; j++)
if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)
g[i][j] =
g[j][i] = 1;
// Start from Jo's house
dfs(0);
// if Bergkirchweih is reached, then happy
if (used[n + 1]) puts("happy");
else puts("sad");
}
return 0;
}